Você já deve ter precisado converter um sinal digital, gerado por um microcontrolador, em um sinal analógico, mas como fazemos isso? É para isso que serve o R2R, um circuito simples, mas muito útil, que usa apenas alguns resistores. Para entendermos seu funcionamentos, primeiro precisamos conhecer sua construção, que esta mostrada no esquemático abaixo.

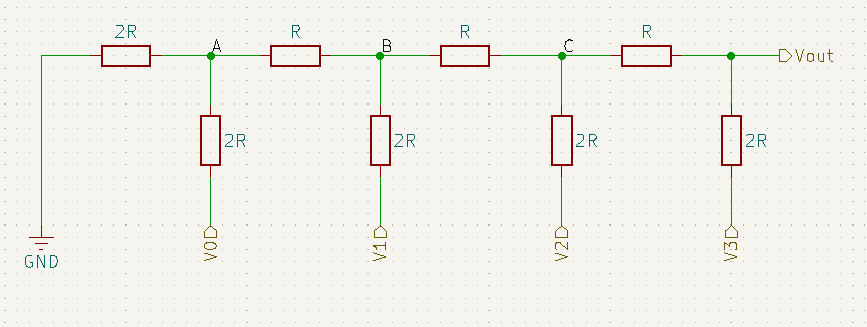
O nome R2R é fácil de entender quando olhamos para o circuito, uma vez que os valores de resistência do circuito alternam entre um resistor de valor R e um com dobro de resistência, 2R. As entradas rotuladas de V0 até V3 são entradas digitais e Vout é a saída desse circuito.

Para usar esse circuito você insere uma palavra binária com V0 sendo o bit menos significativo, e V3 sendo o mais significativo. Como resultado, será obtido uma tensão em Vout, cujo o valor esta entre 0V e um valor de referencia, equivalente a tensão de um bit em nível lógico alto.

Para realizar a analise desse circuito vamos recorrer a 2 princípios bem interessantes da eletrônica, o principio da superposição, e o equivalente de Thévenin.

Calculo da Tensão de Saída em Função das Entradas Para 4 Bits

Considerando, em um primeiro momento, apenas o efeito de V0, temos V1=V2=V3=0. Assim o circuito fica como a imagem abaixo.

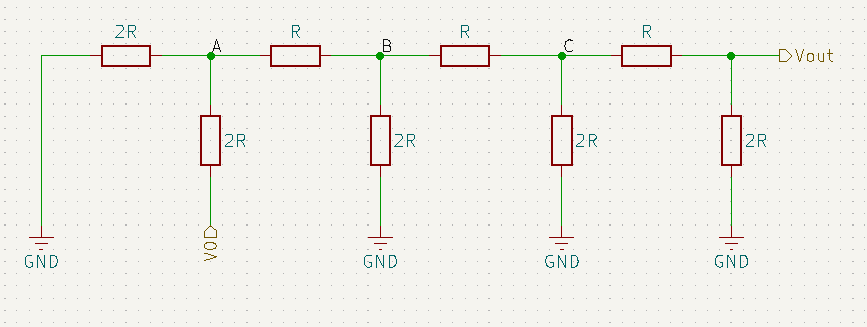
Determinando o equivalente de Thévenin para o ponto A, precisamos primeiro desconectar o restante do circuito, o que nos deixa com o que esta mostrado abaixo.

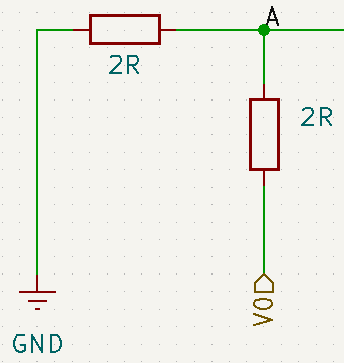
Para este circuito, a resistência de Thévenin é obtida substituindo V0 por 0V, assim a resistência será o paralelo dos dois resistores, ou seja R.

Já a tensão no ponto A ( $V_A$ ) será obtida através do divisor resistivo formado pelos dois resistores de 2R, obtendo-se $V_A=\frac{2R}{2R+2R}V0=\frac{V0}{2}$ , assim, o circuito fica como abaixo.

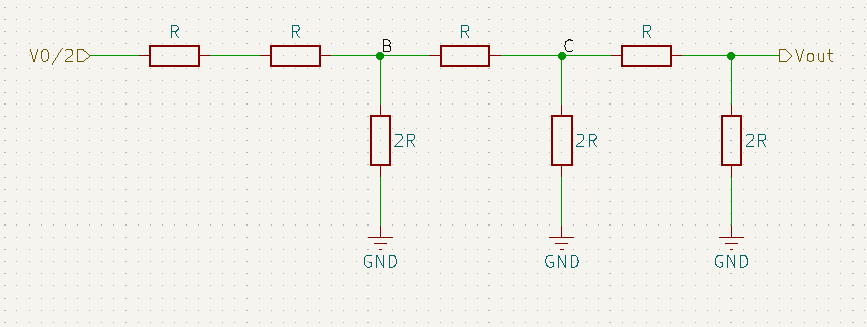
Repetindo essa analise, temos que a tensão no ponto B será $\frac{V0}{4}$ , para o ponto C, $\frac{V0}{8}$ , e por fim, temos que a tensão de saída será $Vout=\frac{V0}{16}$ , quando consideramos o efeito de V0 apenas.

Agora consideraremos apenas a fonte V1, desprezando as demais fontes, o que nos deixa com o circuito abaixo.

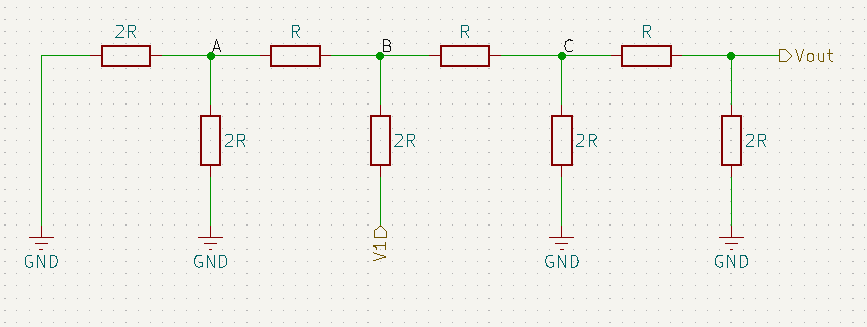
A resistência equivalente até A é dada pelo paralelo dos dois resistores que antecedem esse nó, resultando em um resistor de resistência R, portanto a resistência antes do ponto B é de 2R, o que nos deixa com o circuito abaixo.

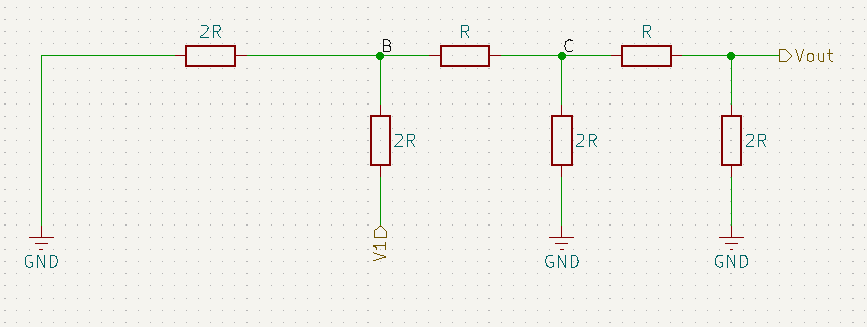
Esse circuito é quase igual ao que tínhamos para V0, logo, de maneira similar ao caso anterior a tensão no ponto B será $\frac{V1}{2}$ . Para o ponto C teremos $\frac{V1}{4}$ , e por fim $Vout=\frac{V1}{8}$ para a saída.

Nesse ponto você já deve ter percebido que o mesmo raciocínio serve para V2 e V3. Considerando cada uma dessas fontes individualmente, teremos $Vout=\frac{V2}{4}$ para V2 e $Vout=\frac{V3}{2}$ para V3.

A tensão na saída considerando todas as fontes é dada pela soma de todas as contribuições individuais, uma vez que aplicamos o principio da superposição. O que resulta na equação abaixo:

(1) $\begin{equation*}Vout=\frac{V0}{16}+\frac{V1}{8}+\frac{V2}{4}+\frac{V3}{2}\end{equation*}$

Generalizando…

Se quisermos colocar mais entradas no nosso circuito, basta adicionar um novo conjunto de resistores R2R, como mostra a imagem abaixo.

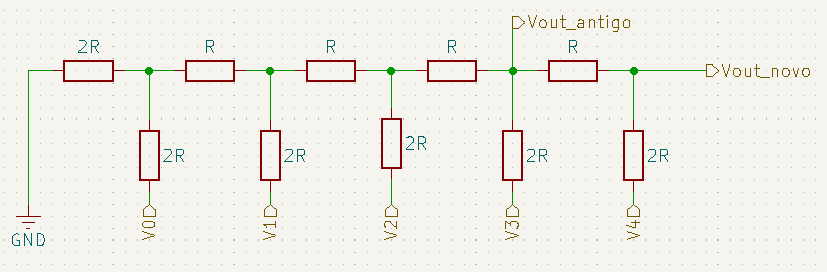
Ao adicionar esses novos resistores à sua rede R2R, a tensão na nova saída (Vout_novo) sem considerar a nova fonte de tensão (V4) será a metade da saída antiga (Vout_antigo). Mas se desprezarmos as demais fontes de tensão, e calcularmos a tensão de saída apenas para V4, encontraremos $\frac{V4}{2}$ . Por fim, aplicamos o principio da superposição novamente, encontrando:

(2) $\begin{equation*}Vout=\frac{V0}{32}+\frac{V1}{16}+\frac{V2}{8}+\frac{V3}{4}+\frac{V4}{2}\end{equation*}$

Se você observar os denominadores das equações 1 e 2, você verá que temos potências de base 2, de forma que $32=2^5$ , $16=2^4$ e assim por diante. Então, a equação anterior pode ser escrita como sendo:

(3) $\begin{equation*}Vout=\frac{V0}{2^5}+\frac{V1}{2^{4}}+\frac{V2}{2^3}+\frac{V3}{2^2}+\frac{V4}{2^1}\end{equation*}$

A fim de generalizar essa expressão, tomaremos o circuito abaixo.

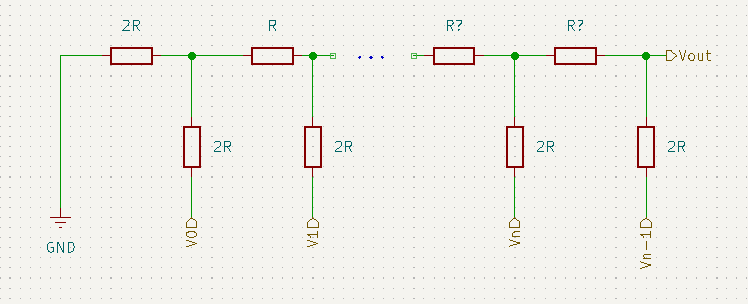
Se você observar as equações 1 e 3, você verá que, quando temos 4 entradas digitais, a contribuição de V0 é dividida por $2^4$ . Já para 5 entradas, temos V0 dividido por $2^5$ , disso concluímos que para n entradas, teremos $\frac{V0}{2^n}$ .

Para V1, temos, $\frac{V1}{2^3}$ para 4 entradas, e $\frac{V1}{2^4}$ para 5 entradas. Assim, para n entradas, ficamos com $\frac{V1}{2^{n-1}}$ .

A entrada mais a direita, sempre ficou dividida por dois, assim, para n entradas, teremos $\frac{Vn-1}{2}$ . Por fim a expressão 3 pode ser reescrita de modo geral como sendo:

(4) $\begin{equation*}Vout=\frac{V0}{2^n}+\frac{V1}{2^{n-1}}+\frac{V2}{2^n-2}+...+\frac{Vn-3}{2^3}+\frac{Vn-2}{2^2}+\frac{Vn-1}{2^1}\end{equation*}$

O R2R é um circuito simples, porém muito útil, capaz de converter sinais digitais em analógicos. E você, já conhecia ele? Deixe seu comentário.

Conhecimento

R2R: Um Conversor Digital Analógico Simples

Calculo da Tensão de Saída em Função das Entradas Para 4 Bits

Generalizando…